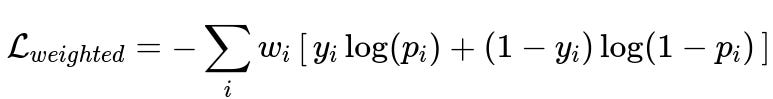ML Interview Q Series: How can you create a model with a very Unbalanced dataset?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Building a model when one class (or several classes) is heavily underrepresented can be challenging. The skew in class distribution can lead to a model that predicts only the majority class correctly, ignoring minority classes altogether. There are different strategies to address this challenge, focusing on data-level adjustments and algorithmic modifications.
Data-Level Approaches
Undersampling the majority class can help rebalance the class distribution by removing instances from the class that dominates. This can reduce the dataset size significantly if the class imbalance is severe, potentially discarding valuable data and features.
Oversampling the minority class by replicating instances of the underrepresented classes can help bring more balance to the distribution. However, if done naively, it may lead to overfitting because the same minority class instances keep reappearing.
Synthetic data generation techniques such as SMOTE or ADASYN create new synthetic minority class data points by interpolating between existing minority samples. This approach can help the model see more diverse examples of the minority class without relying purely on duplication.
Algorithm-Level Approaches
Cost-sensitive learning modifies the training objective to penalize misclassifications of the minority class more heavily. This helps the model focus on correctly classifying rare events. For instance, many libraries allow specifying class_weight='balanced' for algorithms like logistic regression or tree-based methods to automatically scale the loss for each class based on its frequency.
Custom loss functions can be designed to emphasize the minority class. One common method is to use a weighted cross-entropy or focal loss. These loss functions introduce an additional weight or attenuation factor for the minority class.
Below is one of the well-known cost-sensitive learning losses, the weighted cross-entropy. It is especially relevant for unbalanced datasets in binary classification. The model places a higher penalty on misclassifying the minority class:
where w_{i} is the weight applied to the loss for each sample i (which typically depends on whether i belongs to the minority or majority class), y_{i} is the true label (0 or 1), and p_{i} is the predicted probability of the model for the class labeled 1.
Threshold Tuning and Probabilistic Approaches
When using probabilistic models, adjusting the decision threshold can be an effective method to handle imbalance. Instead of defaulting to threshold=0.5, you can tune the threshold to improve metrics such as recall for the minority class. This means that an observation will be classified as the positive/minority class if model_probability > threshold. If the cost of missing a positive instance is high, the threshold can be lowered to capture more minority class instances.
Model Evaluation and Metrics
Using metrics like accuracy can be misleading in heavily imbalanced scenarios, because a naive model that always predicts the majority class may achieve high accuracy. Better metrics include:
Precision and recall, especially if you care more about capturing positive (minority) examples (recall).
F1-score, which combines precision and recall into a single measure.
Precision–recall (PR) curves and the area under this curve (AUC-PR).
ROC curves, but especially focusing on the area under the ROC curve can help if you want a general measure of separability.
Practical Implementation Details
In Python, you can often specify class weights in scikit-learn estimators to handle imbalance. For example, when training a LogisticRegression model:
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(class_weight='balanced')
model.fit(X_train, y_train)
For a more nuanced approach (like custom weights), you can explicitly define them:
weights = {0: 1., 1: 10.} # Example, assign heavier penalty to class '1'
model = LogisticRegression(class_weight=weights)
model.fit(X_train, y_train)
In deep learning frameworks such as PyTorch, you can define a weighted cross-entropy loss:
import torch
import torch.nn as nn
weights = torch.tensor([1.0, 10.0]) # For a binary classification problem
criterion = nn.CrossEntropyLoss(weight=weights)
This ensures that misclassifications in the minority class are penalized more during backpropagation.
Common Follow-up Questions
What are the main considerations when choosing between undersampling and oversampling?
Undersampling can cause loss of information if the majority class is significantly larger, potentially weakening your model’s understanding of important aspects of the majority class. Oversampling is simple but can lead to overfitting if not used carefully. Synthetic approaches (such as SMOTE) can be beneficial but require caution about where the new samples are created. You should also consider the computational cost: undersampling reduces dataset size, so it is faster, whereas oversampling maintains or expands data size, increasing training times.
Why might weighted loss functions or cost-sensitive learning be preferable to data-level techniques?
Altering data distribution via undersampling or oversampling might remove useful patterns or introduce duplicated (or synthetic) points, which can distort your representation of the data manifold. Cost-sensitive learning keeps your dataset intact and focuses on directly adjusting the loss function. This often leads to more natural adjustments of the decision boundary. However, you should be mindful when selecting the weight hyperparameters. An incorrect weighting can cause the model to swing too heavily toward the minority class or ignore it if the weights are not chosen properly.
How do you choose the optimal threshold in the presence of class imbalance?
Selecting an optimal threshold typically involves plotting metrics such as precision vs. recall at various thresholds, or examining the F1-score across thresholds. Another approach is to optimize for a specific cost function that incorporates your application’s priorities: for example, if you place a high cost on false negatives, you might shift the threshold to ensure fewer minority-class cases are missed. You can systematically evaluate different thresholds using a validation set or cross-validation and select the one that yields the best trade-off between precision and recall.
When would you use focal loss in practice?
Focal loss is particularly effective in scenarios with severe class imbalance or when there are a large number of easy negatives in the data. Instead of giving equal importance to every sample, focal loss adds a modulating factor that reduces the loss contribution of well-classified examples, allowing the model to focus more on misclassified or hard examples. This technique is especially popular in object detection tasks (for instance, the RetinaNet architecture).
How can you ensure that your model does not overfit when using SMOTE or other synthetic data generation methods?
Overfitting can happen if the newly created synthetic samples are too similar to each other or to existing samples, effectively reducing the diversity of the training set. You can address this by carefully selecting hyperparameters in SMOTE or ADASYN that control how synthetic points are generated. You may also consider a more refined technique (e.g., SMOTE variants that take feature space density into account), and use proper cross-validation to ensure your model generalizes. Finally, combining synthetic data approaches with cost-sensitive learning or threshold tuning can create a more robust pipeline.
What is the significance of using metrics like AUC-PR instead of AUC-ROC for imbalanced datasets?
The ROC curve can give an overly optimistic view in highly imbalanced scenarios because the false positive rate might remain small even if the absolute number of false positives is substantial. PR curves, on the other hand, focus on precision and recall. They are more sensitive to the exact performance on the positive (minority) class. In many imbalanced cases, a high AUC-ROC can coincide with a relatively low precision, meaning the model returns many false positives relative to true positives.
How would you handle multi-class imbalances?
For multi-class scenarios with imbalance, you can apply the same strategies as in the binary case but separately for each minority class. You might use class-wise oversampling, undersampling, or synthetic sample generation. Many libraries also allow specifying per-class weights when computing loss functions, ensuring that each class’s misclassification is penalized according to its frequency in the dataset. You should be mindful that each minority class might have different severity of imbalance and might require tailored weights or sampling strategies.
How do you validate that your approach to handling imbalance is actually helping?
A solid validation scheme is essential. Consider:
Using stratified sampling in cross-validation to preserve the overall class distribution in each fold.
Carefully analyzing relevant metrics (precision, recall, F1-score, AUC-PR) for each class in each fold.
Comparing metrics between models trained with and without imbalance-handling techniques. You can also monitor confusion matrices to see if the minority class predictions are improving or if you are simply shifting errors from one class to another.
A comprehensive strategy that includes careful data partitioning, appropriate metrics, cost-sensitive training, and possible data-level balancing or threshold tuning will usually give the best results in handling an unbalanced dataset.
Below are additional follow-up questions
How do you handle extremely imbalanced datasets where the minority class is only a tiny fraction (e.g., 1 in 10,000) of the data?
When the minority class is exceptionally sparse, even methods like regular oversampling or standard SMOTE might be insufficient because you have so few positive examples to begin with. You might consider advanced synthetic data generation techniques (such as SMOTE variations or GAN-based approaches) that can leverage subtle feature patterns in the minority class. One key pitfall is that if the minority class has genuine diversity (e.g., multiple subtypes within that rare class) but you only have a handful of examples, it can be difficult to capture the full variation. Another challenge is the sheer imbalance makes typical metrics like accuracy or even AUC-ROC less informative. You would likely rely on high-recall metrics, or you might define custom metrics that reflect the rarity of the event. In real-world scenarios, domain knowledge can be crucial for identifying the most relevant features or relationships that separate this sparse minority class from the majority.
What if the minority class data is limited and oversampling is not feasible due to domain constraints?
In certain high-stakes domains (medical, aerospace, finance with highly sensitive anomalies), artificially synthesizing or duplicating data may be prohibited or impractical due to regulatory or domain-specific constraints. In these situations, cost-sensitive learning (using well-chosen class weights or custom loss functions) can be the primary approach. Another approach is transferring relevant representations learned on a broader dataset and then fine-tuning carefully on the limited data you have. Pitfalls include overfitting if the amount of minority data is extremely small or if domain shift occurs (i.e., the pre-trained model’s domain differs from your target domain). In practice, it is essential to collaborate with domain experts to ensure the minority class data are accurately labeled and that any form of data augmentation is valid in the real-world setting.
How do you handle concept drift in a real-time data stream where the minority class may change over time?
Concept drift occurs when the underlying data distribution shifts over time, potentially altering the characteristics of both majority and minority classes. A model trained on historical data might degrade in performance if the minority class evolves to have new patterns. A practical approach is to use an incremental or online learning model that updates its parameters as new data comes in, possibly recalculating class weights or applying online oversampling on recent batches. A pitfall is that if you rely on fixed oversampling or static class weights, you risk becoming outdated as the distribution changes. You need a strategy for continuous evaluation (e.g., streaming metrics, sliding windows for validation) to detect drift early. Additionally, you can keep an adaptive sampling mechanism that can raise a flag whenever the minority-class pattern changes significantly, prompting model retraining or re-weighting.
How do you interpret a confusion matrix in a severely imbalanced scenario, and what pitfalls might occur?
In extremely imbalanced settings, the number of true negatives in the confusion matrix can be enormous, while true positives are scarce. This can make the false positive rate look deceptively low. Interpreting the confusion matrix requires a careful look at absolute numbers rather than just the percentages. A pitfall is that an apparently high overall accuracy or a low false positive rate might mask the fact that the model is missing almost all minority examples. Another subtlety is that if the minority class is crucial (e.g., fraud detection), even a small number of missed positive cases (false negatives) can be costly. Looking at additional rows and columns in the confusion matrix (specifically the row or column for the minority class) and coupling it with more informative metrics like recall, F1-score, or the precision-recall curve is essential to fully understand performance.
How do ensemble methods help tackle class imbalance, and what are potential pitfalls?
Ensemble methods (like boosting, bagging, or stacking) can help address imbalance by combining multiple models that each might learn different aspects of the minority class. Techniques such as RUSBoost (Random Under Sampling combined with AdaBoost) or SMOTEBoost (SMOTE combined with AdaBoost) specifically incorporate sampling strategies into an ensemble learning pipeline. These methods often enhance performance by reducing variance and bias in the estimates for the minority class. A potential pitfall is that if the base learners are all trained on heavily imbalanced subsets or if sampling is poorly implemented, the ensemble might not add meaningful diversity. There is also a computational overhead; ensemble methods require training multiple models. When data is extremely scarce, building large ensembles can also risk overfitting the minority class, especially if synthetic oversampling is too aggressive.
What role does domain knowledge play when generating synthetic samples for the minority class?
Domain knowledge can be the deciding factor in whether synthetic data generation is valid and effective. In some fields, you might know that linear interpolation (such as standard SMOTE) between minority class samples is nonsensical. Instead, you might incorporate constraints that govern which points in feature space are realistic. For instance, in medical imaging, you might need advanced augmentation techniques that mimic anatomically plausible variations. Pitfalls arise if synthetic data violates real-world constraints, leading the model to learn patterns that do not correspond to actual minority instances. Overreliance on naive synthetic sampling without domain verification can degrade performance in practical scenarios, especially if the minority class distribution is more complex than the oversampling algorithm can handle.
How do you handle noisy or mislabeled data in the minority class?
When the minority class is inherently small, even a few mislabeled instances can significantly impact your model. If you apply oversampling or synthetic approaches to data with mislabeled points, you risk propagating errors. One approach is to perform data cleaning or advanced outlier detection in collaboration with domain experts before applying any class balancing. In cases where it is hard to verify labels, you might adopt a robust loss function or outlier-aware technique that reduces the impact of suspicious samples. The pitfall is ignoring label noise can cause your model to learn highly misleading characteristics about the minority class or systematically discount it entirely. Additionally, it may falsely inflate your sense of the model’s performance if you do not conduct thorough validation with carefully verified labels.
How can transfer learning be applied to address class imbalance, and what are the edge cases?
Transfer learning involves starting with a model pre-trained on a large, possibly related dataset, and then fine-tuning on your imbalanced data. Because many of the model’s layers already capture general features, you might only need a smaller number of minority samples in your target task to achieve reasonable performance. Edge cases arise if the source domain is too dissimilar from the target domain, causing negative transfer. Another subtlety is deciding which layers to freeze. Freezing too many layers might prevent the model from adapting to minority-specific features in your data; freezing too few can lead to overfitting if your minority class data is very limited. As with other methods, domain knowledge is key. If you know the pre-training data share certain key patterns (e.g., for images, similar backgrounds or shapes), then fine-tuning a subset of layers might be sufficient to capture the minority class features.
How do you manage class imbalance when it extends to multiple minority classes of different severities?
Multi-class imbalance can be more complicated when multiple classes each have different sample sizes, and some are extremely underrepresented. Simple strategies like specifying a single global weight for “minority” classes may not be sufficient. Instead, you might give each class a different weight proportional to 1 / (frequency of the class). For data-level interventions, you could apply class-specific sampling or generation approaches. Pitfalls include inadvertently creating overlaps among synthetically generated classes or oversampling a single class to the point that it overwhelms other minorities. In practice, an iterative approach may be necessary, with repeated experiments checking confusion matrices for each class separately, ensuring that improvements in one minority class do not come at the expense of performance on another.
How would you systematically select hyperparameters (such as class weights or SMOTE parameters) in an imbalanced dataset scenario?
Systematic hyperparameter tuning can be done via cross-validation, but you need stratified folds to preserve class proportions in each fold. For class weights, you might define a range or formula (for example, weighting each class proportionally to 1 / (class frequency)^alpha) and grid search over different alpha values. For SMOTE, you would adjust parameters like the k-neighbors used for generating synthetic points. The main pitfalls arise when your cross-validation splits are not representative, leading to inflated performance metrics that do not generalize. Another challenge is that each metric (e.g., F1, recall, precision, AUC-PR) might lead you to different optimal parameter settings. You also must watch out for computational cost if you are performing large-scale searches, and sometimes a carefully reasoned approach or smaller search space can be more efficient.
How do you ensure your imbalanced classification system remains robust and fair, especially if it directly affects individual lives?
In high-stakes decisions like hiring, lending, or healthcare, you must examine fairness metrics (for instance, disparate impact or equal opportunity) in addition to performance metrics. An imbalanced dataset might reflect historical biases, and oversampling or synthetic data generation might amplify those biases if not carefully controlled. For instance, if the minority class is also a protected group, you need a more holistic approach that includes fairness constraints or the removal of harmful biases from training data. Pitfalls include inadvertently making your model less accurate for certain subgroups or ignoring intersectional effects (e.g., a subgroup that is extremely rare in the dataset). Ongoing monitoring of model outcomes, ethical reviews, and domain expert consultations are typically required to maintain fairness and transparency in real-world imbalanced classification tasks.