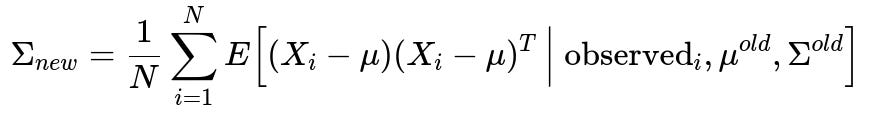📚 Browse the full ML Interview series here.
Comprehensive Explanation
When data has missing entries, directly computing a sample covariance matrix becomes non-trivial. We typically cannot just apply the usual covariance formula because many data points are incomplete. Several methods are commonly used:
Listwise Deletion
This is the simplest approach, where you discard any row that has at least one missing value. However, this reduces the effective dataset size significantly and can introduce bias if the missing data are not missing completely at random.
Pairwise Deletion
This method computes the covariance for each pair of features based on all available data for that pair. While it uses more data than listwise deletion, the resulting covariance matrix can sometimes become non-positive semidefinite, especially if the missingness is substantial or non-random.
Maximum Likelihood Estimation with EM Algorithm
A robust technique to handle missing data is to use the Expectation-Maximization (EM) algorithm under the assumption of multivariate normality. The idea is:
E-Step: Estimate the missing values given the current estimates of the mean vector and covariance matrix (i.e., compute the expected sufficient statistics).
M-Step: Update the mean and covariance estimates using the expectations from the E-Step.
The core update for the covariance matrix after the E-step is illustrated by the expected outer product of mean-centered data, where missing entries are integrated out according to the current parameter estimates:
Here:
N is the total number of data points (including those with partial missingness).
X_{i} is the i-th data vector, which might have some components missing.
observed_{i} refers to the actually observed components of X_{i}.
mu^{old} and Sigma^{old} are the estimates of the mean and covariance from the previous iteration.
E[ (X_{i}-mu)(X_{i}-mu)^{T} | observed_{i}, mu^{old}, Sigma^{old} ] is the conditional expectation of the complete-data outer product for the missing entries.
By iterating between computing these expectations (E-step) and updating mu and Sigma (M-step), the estimates typically converge to a maximum-likelihood solution for the covariance.
Multiple Imputation
Another robust approach is to impute the missing entries multiple times to create several "complete" datasets. Each dataset is then used to compute a covariance matrix. Finally, the covariance matrices are pooled to obtain a more reliable estimate. This requires more computational overhead but can yield less biased estimates when compared to single imputations.
Practical Implementation Considerations
If the missing pattern is random and you have enough data, EM or multiple imputation usually yields more efficient estimates of the covariance matrix.
If the data are missing systematically (not at random), no method can fully correct the bias introduced by non-random missingness without additional information.
Common Follow-up Questions
How does EM specifically handle different missing patterns?
The EM algorithm relies on the assumption that, conditionally on observed data and current parameter estimates, the missing values can be predicted from a multivariate distribution (typically a conditional Gaussian). No matter how the missingness is distributed across the data matrix (e.g., some rows with multiple missing features, others with single missing features), the E-step uses the model’s conditional distributions to estimate those entries. As long as missingness is not completely deterministic or adversarial, EM incorporates all partial information effectively.
In practice, EM can handle arbitrary patterns of missingness, but convergence speed and final accuracy can be sensitive to the fraction of missing values. If too many entries are missing or the pattern is heavily skewed, the estimates might be less stable and require regularization or strong priors.
Why not just use pairwise deletion to compute the covariance matrix?
Pairwise deletion can make better use of the available data than listwise deletion, but it can lead to several pitfalls:
The resulting covariance matrix might not be positive semidefinite, which is problematic for subsequent linear algebra operations.
Different pairs of features can leverage different subsets of samples, potentially introducing inconsistencies in the estimate.
It does not account for the correlations among all variables when missingness is present. EM, on the other hand, uses a global view by modeling the entire covariance structure.
Could multiple imputation be more robust than EM?
Multiple imputation can be more robust in certain scenarios, particularly if:
You want to capture the inherent variability of the missing values in the final estimates, rather than a single "plug-in" estimate of the missing entries.
You prefer to do further analyses (like regression on imputed datasets) and then combine results across multiple runs.
However, multiple imputation is computationally more expensive. EM provides a single covariance estimate but does not explicitly account for the uncertainty of each imputed entry. Multiple imputation accounts for that uncertainty by creating multiple plausible versions of the missing data.
What if the data are not normally distributed?
The EM algorithm typically assumes a multivariate normal distribution to compute the conditional expectations of missing entries. If the true distribution is heavily skewed or not approximately Gaussian, the covariance estimates might be biased. In that case:
You could apply suitable transformations to make the data more normally distributed.
You could rely on more general algorithms, like some nonparametric imputation methods, but these might be more complex than classic EM.
How to implement a basic EM approach or imputation in Python?
Below is an illustrative code snippet showing how you might use IterativeImputer (a scikit-learn approach loosely based on an iterative procedure akin to EM in spirit) to handle missing data, then compute a covariance matrix:
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
# Suppose X is a numpy array with missing values denoted by np.nan
# Example shape: (num_samples, num_features)
# Create some synthetic data for illustration
np.random.seed(42)
X = np.random.randn(10, 3)
X[2, 1] = np.nan # artificially introduce some missing values
X[5, 2] = np.nan
# Initialize the iterative imputer
imputer = IterativeImputer(max_iter=10, random_state=0)
X_imputed = imputer.fit_transform(X)
# Compute the covariance matrix on the imputed data
cov_matrix = np.cov(X_imputed, rowvar=False)
print("Imputed Data:\n", X_imputed)
print("Covariance Matrix:\n", cov_matrix)
This snippet uses a built-in iterative approach. Under the hood, each feature with missing values is regressed against other features, and the predictions are used to fill missing entries. It iterates this step multiple times until convergence. After imputation, you have a complete dataset and can easily compute the covariance matrix.
Pitfalls and Edge Cases
If a large portion of your data is missing, imputation-based methods can introduce high uncertainty. Regularization or Bayesian methods can help stabilize estimates.
If the missing data mechanism is "Missing Not at Random" (MNAR), none of these methods can fully correct the bias without modeling the missingness process itself.
With small sample sizes and many missing entries, you can easily overfit the missing data with elaborate models. Cross-validation or out-of-sample validation can help detect this issue.
Always consider domain knowledge to guide the choice of method (e.g., normality assumptions, plausible value ranges, relevant side information).
By leveraging these techniques, you can systematically estimate a covariance matrix from data containing missing values while minimizing bias and variance in your final estimates.
Below are additional follow-up questions
How do we ensure that the EM-estimated covariance matrix remains positive definite?
When using the EM algorithm to estimate a covariance matrix with missing data, one major concern is ensuring that the updated covariance matrix does not become singular or indefinite. Under typical implementations of EM with a multivariate normal assumption, the derived covariance matrix should remain positive definite. However, several factors can disrupt this guarantee:
Numerical Precision: In computational practice, floating-point inaccuracies can cause near-singular matrices if the dataset is small or if multicollinearity is present.
High Dimensionality Compared to Sample Size: If the number of features is large relative to the number of samples, the covariance matrix can be ill-conditioned, leading to near-singular updates.
Inappropriate Initialization: If you initialize with a poorly conditioned covariance matrix or if your data are heavily missing, early EM iterations can produce degenerate estimates.
To address these issues, one can:
Regularize the Covariance Matrix: Add a small value (lambda) to the diagonal of the covariance matrix during updates to maintain numerical stability. This technique is sometimes referred to as shrinkage.
Use a Factor or Low-Rank Model: If you suspect the data lie on a lower-dimensional manifold, factor-based covariance estimation can reduce the dimensionality and stabilize the matrix.
Monitor Condition Number: After each M-step, check the condition number of the covariance matrix. If it exceeds a threshold, consider applying correction steps such as eigenvalue clipping or diagonal loading.
These strategies help ensure that you end up with a well-conditioned covariance estimate.
What if the fraction of missing data is extremely high?
When a large percentage of entries are missing, the reliability of any imputation or estimation procedure can be severely compromised. A few potential outcomes and strategies include:
Uncertain Estimates: Even EM might converge, but the standard errors of the estimated parameters can be large, and the covariance matrix could be unstable. Confidence in any statistical inference decreases sharply.
Biased Estimates if Missing Not at Random: In practice, if missingness is systematic or MNAR (Missing Not at Random), you might be introducing unknown biases that no standard algorithm can fix without additional assumptions or observed data about the missingness mechanism.
Regularization or Dimensionality Reduction: With very sparse observations, techniques like latent factor modeling or principal component analysis (PCA) combined with EM-based estimation may yield more robust estimates than trying to estimate a fully dense covariance matrix.
Leverage External or Auxiliary Data: In real-world scenarios, you might be able to combine partial information from multiple sources, such as multiple sensors or prior domain knowledge, to reduce uncertainty and guide imputation.
Ultimately, if missingness is too extensive, you have to question whether the dataset is salvageable. It might be more cost-effective to collect additional data rather than continue with unreliable estimates.
Could domain constraints or structure be incorporated into the covariance estimation?
In many real-world problems, especially in fields like finance, biology, or physics, there are known structures or constraints on how variables relate to each other. Examples include:
Known block structure in the covariance (e.g., certain groups of features should be highly correlated while others should be uncorrelated).
Known sparsity or low-rank assumptions (e.g., in genomics, certain large-scale correlation patterns arise from small sets of latent factors).
One can incorporate such constraints by:
Structured Covariance Models: Assume that the covariance matrix has a known parametric form (such as a block-diagonal or Toeplitz structure). During EM, constrain the updates so that the estimated covariance adheres to that structure.
Graphical Models: Use Gaussian Markov Random Fields, where conditional independence assumptions translate to a sparse precision matrix (the inverse of the covariance). EM can be adapted by imposing penalties on the precision matrix to enforce sparsity.
Bayesian Priors: In a Bayesian approach, impose priors on the covariance matrix that capture domain knowledge (e.g., Wishart priors, shrinkage priors). Missing data are then integrated out in a principled way, though computations can become more involved.
By enforcing realistic structure, you often gain more stable estimates and reduce the dimensionality of the parameters, thus improving convergence when data are missing.
Are there non-iterative approaches to covariance estimation with missing data?
While EM-like iterative methods are standard, certain non-iterative approaches exist for specific conditions:
Single Imputation with Regression: For each missing feature, train a simple regression model using other features as predictors. Fill in all missing values once and then compute the covariance on the completed dataset. This method is not truly “closed-form” but may require only one pass if you do not iterate the imputation.
Pairwise Complete Observations with Post-Processing: You could compute pairwise covariances and then adjust the matrix to ensure positive semidefiniteness, for instance by projecting onto the nearest positive semidefinite matrix. This approach is somewhat heuristic and can still yield biases if the missingness patterns are non-random.
Analytical Marginalization (Special Cases): In rare settings with known parametric forms for the missingness, there might be closed-form solutions to the expected outer products. However, these solutions are typically restricted to very simple missing data patterns or specialized distributions.
Such non-iterative methods can be faster or easier to implement, but often do not incorporate the same level of statistical rigor or convergence guarantees as the EM algorithm or multiple imputation.
How do we handle missing data in a time-series context for covariance estimation?
Time-series data can have additional structure and complexities:
Temporal Dependencies: Observations are not independent across time. A gap in one time step may carry over or correlate with gaps in future steps.
Non-Stationarity Issues: The mean and variance of a time series can change over time, complicating straightforward assumptions of a single global covariance matrix.
Irregular Sampling: Missing data in time series may cause irregular time intervals that standard covariance formulas do not account for.
Possible approaches include:
State-Space Models / Kalman Filters: These methods naturally handle missing observations by performing prediction-update steps. The Kalman filter can estimate latent states and their covariance matrices even with partial or missing observations at each time step.
EM with a Time-Series Model: Incorporate an autoregressive or state-space structure directly into the EM framework. The E-step involves inferring missing states or missing measurements, and the M-step updates parameters of the time-series model.
Interpolation / Smoothing: For data with small gaps, interpolation methods (such as spline interpolation) might fill in missing time points before covariance computation. However, interpolation may introduce biases if the data are missing systematically.
An important pitfall arises when ignoring temporal correlation and simply treating each point as an i.i.d. sample. Doing so can yield inaccurate estimates of covariance, especially when the patterns of missingness interact with strong temporal trends.
How do model-based vs. algorithmic imputation methods (e.g., random forest imputation) compare for covariance estimation?
Algorithmic imputation methods like random forest imputation (often called MissForest) do not explicitly assume a particular distribution (like Gaussian). Instead, they model the relationship between features using decision trees. For covariance estimation:
Pros: They can capture complex, nonlinear relationships among features, potentially leading to more accurate predictions of missing values than linear methods, especially when the data are not normally distributed.
Cons: They do not directly produce an estimate of the covariance matrix. Instead, you first fill in the missing entries and then compute a sample covariance on the completed data. This approach does not typically incorporate parameter uncertainty in the final covariance estimate.
Pitfalls: If the fraction of missing data is high, random forests might overfit the observed data when predicting missing entries, thus biasing the covariance. Also, large computational overhead is required for repeated tree-based modeling when the dataset is large.
In scenarios where you strongly suspect non-Gaussian relationships or have substantial domain knowledge that certain nonlinearities exist, a random forest approach can be more robust. But if you want a statistically principled estimate of covariance with uncertainty accounted for in a single iterative framework, a model-based approach like EM remains standard.
Does scaling or standardizing data before imputation affect the covariance estimation?
Standardizing each feature (subtracting mean and dividing by standard deviation) or otherwise scaling the data before imputation can influence the accuracy of the estimated covariance:
Better Numerical Stability: Scaling can help certain algorithms converge more reliably, especially methods that involve regression or iterative updates sensitive to large feature magnitudes.
Interactions with Missingness Patterns: If a feature has many missing values, computing a good estimate of its standard deviation from the observed entries might be misleading if those entries are not representative. This could result in incorrect scaling and biased imputations.
Reverse-Transformation: If you do scale data, remember that after imputation and covariance estimation, you may need to transform back to the original feature space. This re-transformation can affect the final covariance estimates.
A practical approach is to ensure that when you do scale data, you compute the scaling parameters (mean, standard deviation) in a way that accounts for missingness (e.g., using only the available values). EM-based or multiple imputation approaches can also estimate scaling factors as part of the procedure, leading to more self-consistent results.
How do we validate whether our imputed covariance matrix is accurate?
Validation of an imputed covariance matrix can be tricky because ground truth is typically unknown once data are missing. Still, some approaches include:
Simulation Study: If you can artificially introduce missingness in a fully observed dataset (where you know the true covariance), you can compare your imputed result to the ground truth. This helps you see how well your method handles realistic missingness patterns.
Predictive Checks: Use the covariance matrix in a downstream task (e.g., classification, regression, portfolio optimization). If performance improves or remains stable compared to simpler approaches (e.g., listwise deletion), this is evidence that the imputed covariance might be more faithful.
Residual Analysis: After imputing missing values, look at the distribution of residuals in a regression context. Systematic patterns may indicate that the imputation (and thus the covariance estimate) is missing critical structure.
Cross-Validation: If the data are plentiful and the missingness is not too extreme, you can partition your dataset, artificially mask some known entries, impute them, and compare them with the true values.
These methods highlight subtle failures in your imputation or covariance estimation process, especially if your model incorrectly assumes a distribution that doesn’t match the real data.
Can we utilize robust statistics to handle outliers along with missing data?
In real-world data, outliers can coexist with missingness and skew the covariance estimate. A robust approach might downweight outliers to produce a more stable covariance matrix. Typical robust methods include:
M-Estimators: These approaches use a loss function that is less sensitive to outliers when computing means and covariance structures.
Robust EM: Adapt the EM algorithm so that at each iteration, outliers contribute less to the parameter updates. This can be done by modifying the likelihood function or using a heavy-tailed distribution (e.g., multivariate Student-t instead of Gaussian).
Trimmed or Winsorized Imputation: Before or during imputation, extreme values are trimmed or winsorized so that imputed estimates are less sensitive to large outliers.
The pitfall is deciding which observations qualify as outliers and ensuring that large-scale missingness combined with outlier handling does not eliminate too much information. Nonetheless, robust approaches can significantly improve covariance estimates in contaminated datasets.
What are best practices for reporting results of covariance estimation with missing data?
When presenting results, it is crucial to be transparent about the approach taken and the assumptions involved:
Document the Missingness Mechanism: State whether data are assumed Missing Completely at Random (MCAR), Missing at Random (MAR), or Missing Not at Random (MNAR). Clarify any domain-specific justifications for these assumptions.
Describe the Imputation or Estimation Method: Include enough detail for someone else to replicate your procedure (e.g., mention that you used an EM algorithm with a certain convergence threshold, or a random forest imputation with specific hyperparameters).
Quantify Uncertainty: If possible, report confidence intervals or standard errors for the covariance estimates. In multiple imputation, you can show the between-imputation variance.
Perform Sensitivity Analyses: Show how robust the covariance matrix is to different assumptions or methods. If small changes in the imputation procedure drastically alter the covariance, that flags high uncertainty.
Being thorough with these reporting practices helps others interpret and trust the final covariance estimates, especially in critical applications such as risk modeling or policy-making.