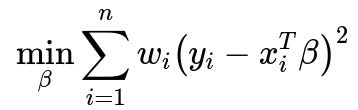ML Interview Q Series: How would you detect Heteroskedasticity?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Heteroskedasticity refers to the condition in which the variance of the error terms in a regression model is not constant across observations. In ordinary least squares linear regression, one of the key assumptions is that the error variance is constant. When this assumption is violated, the model’s statistical inferences (standard errors, confidence intervals, hypothesis tests) can be misleading. Detecting heteroskedasticity is therefore vital for ensuring the validity and reliability of your regression analysis.

A common way to detect heteroskedasticity is through diagnostic plots. For instance, you can plot the residuals of your regression against the fitted values or against individual predictors. If the residual variance appears to grow or shrink systematically across the range of fitted values, it suggests heteroskedasticity. However, relying solely on visual inspection is subjective, so more formal tests exist.

Another widely used method is the Breusch-Pagan test (and its variants such as Koenker-Bassett). You typically run your initial regression, collect the residuals, and then fit an auxiliary regression of the squared residuals on the same predictors (or sometimes on a subset or a transformed set of predictors). The test statistic is based on the explanation power (R^2) of that auxiliary regression.

Breusch-Pagan Test Statistic

Below is the core formula for the Breusch-Pagan test statistic that is often considered central for detecting heteroskedasticity in a linear regression setting.

where T is the test statistic, n is the sample size (number of observations), and R^2_{aux} is the coefficient of determination from the auxiliary regression of the squared residuals on the predictors. Under the null hypothesis of homoskedasticity, T is approximately chi-square distributed with degrees of freedom equal to the number of predictors (excluding the intercept) in the auxiliary regression. A high value of T relative to the chi-square distribution critical value indicates potential heteroskedasticity.

In practice, there are multiple steps: First, fit the ordinary least squares model and extract the residuals. Second, compute the squared residuals. Third, fit the auxiliary regression of squared residuals on the predictors. Finally, compute the test statistic as above.

Another formal test is White’s test, which generalizes the idea by regressing squared residuals not just on the original predictors but also on their cross-products. White’s test can detect more general forms of heteroskedasticity (including model misspecification that manifests as heteroskedasticity).

A quicker (though less formal) detection method is to examine the residuals vs. fitted-values plot. If there is a clear pattern where the variability of residuals increases or decreases systematically, that is a strong indication of heteroskedasticity.

Example Code Snippet in Python

import numpy as np
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan

# Suppose X is your matrix of predictors and y is your target
X = sm.add_constant(X)
model = sm.OLS(y, X).fit()
residuals = model.resid

# Perform Breusch-Pagan test
test_results = het_breuschpagan(residuals, model.model.exog)

# test_results returns (LM stat, LM p-value, F-stat, F p-value)
print("Breusch-Pagan p-value:", test_results[1])

In this code, if the p-value is very small, you have statistically significant evidence of heteroskedasticity. If it is large, you do not reject the homoskedasticity assumption.

Why Visual Inspection is Not Sufficient

Relying solely on a residuals vs. fitted plot can be misleading if there are many data points or if the patterns are subtle. Formal tests like Breusch-Pagan or White’s test provide a more objective indication of heteroskedasticity. However, it is often a good idea to perform both graphical diagnostics and formal tests for a well-rounded analysis.

Potential Pitfalls and Edge Cases

One pitfall is that the standard tests can sometimes be sensitive to outliers and model misspecification. If the functional form of your model is incorrect (for example, you are missing a polynomial term or an interaction), you might get patterns in the residuals that appear to be heteroskedasticity but are really due to the model’s inability to capture the true relationship. It is therefore best practice to combine multiple diagnostics to ensure that the patterns in the residuals are not caused by other issues in the model.

Heteroskedasticity can also appear in time series data (often referred to as conditional heteroskedasticity). If your data is time-dependent, specialized models like GARCH (Generalized AutoRegressive Conditional Heteroskedasticity) might be more suitable for capturing volatility clustering.

Follow-up Questions

How does heteroskedasticity affect inference in linear models?

Heteroskedasticity can lead to biased estimates of the standard errors. When the variance of the error terms is not constant, the usual ordinary least squares assumption that underpins the calculation of confidence intervals and p-values is violated. As a result, the model might underestimate or overestimate the variability of the coefficient estimates, leading to incorrect conclusions about statistical significance.

One way to mitigate this is to use heteroskedasticity-robust standard errors (also called White’s standard errors). These robust standard errors adjust the covariance matrix for non-constant error variance and can help restore valid inference even when heteroskedasticity is present.

Why might we prefer one test over another (Breusch-Pagan vs. White’s test)?

Breusch-Pagan typically involves regressing squared residuals on the original predictors and testing for significance of that auxiliary regression. White’s test further includes not just the original predictors but also their squares and cross-terms. This allows White’s test to detect more general forms of heteroskedasticity but also can reduce power if the model includes many predictors, since you are adding more terms into the auxiliary regression.

In practice, you might try both: if you suspect your errors have a simple multiplicative form of heteroskedasticity (for example, error variance scaling with a single predictor), then Breusch-Pagan might suffice. If you suspect more complex patterns, White’s test can be more thorough.

What can you do if heteroskedasticity is found?

You could transform your dependent variable or predictors in a way that stabilizes the variance. For instance, if errors grow with the square of a predictor, a log transformation might reduce heteroskedasticity. You could use heteroskedasticity-robust standard errors to ensure that your coefficient standard errors (and hence your inference) remain valid. You could also switch to different modeling techniques, such as generalized least squares, which explicitly account for known forms of heteroskedasticity.

How would you handle outliers that might be causing heteroskedasticity?

You could first investigate whether the outliers are due to data collection errors or other anomalies that can be corrected or removed. If the outliers genuinely belong to the data distribution, robust regression techniques like RANSAC or quantile regression might be better than standard OLS for dealing with heteroskedastic error structures driven by extreme values. Data transformations, like log or Box-Cox, can sometimes normalize the distribution and reduce the effect of outliers and variance inflation if that transformation is appropriate for the domain.

Why is it important to combine multiple diagnostics?

No single test or diagnostic provides an infallible indication of heteroskedasticity. Residual plots can reveal certain patterns but might miss subtler ones. Formal tests like Breusch-Pagan or White’s test can identify potential heteroskedasticity but can sometimes be influenced by model misspecification or outliers. By combining both graphical diagnostics and formal tests, you reduce your risk of drawing incorrect conclusions about the homoskedasticity assumption.

Using multiple lines of evidence, along with domain knowledge, helps you judge whether apparent violations of assumptions are genuinely due to heteroskedasticity or the result of some other modeling issue (such as unaccounted-for nonlinearities, missing features, or data quality problems).

Below are additional follow-up questions

When do we consider Weighted Least Squares (WLS) to address heteroskedasticity, and how does it work?

Weighted Least Squares is particularly useful when you have a reasonable guess or knowledge about how the error variance scales with certain variables. If you suspect, for example, that variance grows proportionally with some observable factor (like a predictor), you can assign lower weights to observations with higher variance and higher weights to those with lower variance.

In practice, you start by modeling or estimating the relationship between the error variance and some function of the predictors. For instance, you might notice that residual variance grows in proportion to x_i^2 for some predictor x_i. You then define weights w_i = 1 / var(error_i). These weights are applied to each observation when solving the regression.

Below is the core formula for Weighted Least Squares that you might see as the objective function:

where w_i is the weight for observation i, y_i is the observed outcome, x_i is the predictor vector for observation i, and beta is the coefficient vector. By assigning w_i in inverse proportion to the error variance, you effectively “balance” the influence of different points, mitigating the impact of non-constant error variance.

A subtlety arises when w_i must be estimated. If your estimate of var(error_i) is inaccurate, you might over-correct or under-correct. In some real-world cases, you iterate: first fit a model, estimate var(error_i) from residuals, then refit with those variance estimates as weights, and possibly repeat. However, iterative weighting can be sensitive to outliers and modeling assumptions about the variance function.

How do we interpret tests for heteroskedasticity in the presence of correlated errors?

If your residuals are correlated—perhaps due to time-series effects or spatial correlation—then classic tests for heteroskedasticity (such as Breusch-Pagan or White’s test) can yield misleading results. These tests typically assume that error terms are independent. Correlation among error terms can inflate or deflate the test statistic in unpredictable ways.

In such cases, you might need specialized tests or robust approaches that account for both heteroskedasticity and correlation. For time-series data, for example, you could use Newey-West standard errors, which provide robustness against both heteroskedasticity and autocorrelation. Alternatively, you might switch to models that explicitly incorporate correlation structures (e.g., mixed models with random effects, or autoregressive integrated moving average models in time-series analysis).

Pitfalls include misinterpreting a positive test for heteroskedasticity when in reality the main issue is autocorrelation. Another edge case is when the data show both strong correlation and severe non-constant variance, meaning you need to correct for both simultaneously to achieve valid inference.

How can higher-order terms or interactions mask or create heteroskedasticity?

When you include polynomial or interaction terms, you effectively allow your model to capture more complex relationships. Sometimes, failing to include these terms can make it seem like the error variance changes with x_i, when in fact the deterministic part of the model is simply misspecified. Conversely, including an unnecessarily high degree of polynomial or irrelevant interaction can create artificial “residual patterns” that resemble heteroskedasticity, especially in limited data regimes.

An important subtlety arises when polynomial terms lead to extreme predicted values for certain ranges of x_i. The residuals in those regions can become larger or smaller, generating an apparent pattern in the residuals vs. fitted-values plot. This pattern might vanish if you revert to a simpler model or apply a transformation. Checking model fit carefully (e.g., using cross-validation to avoid overfitting) can help you detect when your polynomial or interaction expansions are causing or hiding heteroskedastic-like patterns.

Could you explain the difference between unconditional heteroskedasticity and conditional heteroskedasticity?

Unconditional heteroskedasticity refers to variability in the error terms that is present outright, regardless of conditioning on specific values of the predictors or time. You might see this in cross-sectional data where different observational groups inherently have different variances.

Conditional heteroskedasticity, however, is about how the variance of the errors changes once you condition on certain values of the predictors (or on past information in a time-series context). A classic time-series example is volatility clustering in financial data, where large shocks lead to larger subsequent volatility. This phenomenon is captured by models such as GARCH (Generalized AutoRegressive Conditional Heteroskedasticity). In GARCH, the variance at time t depends on the magnitude of the errors at previous time steps, making it explicitly conditional on the past.

A real-world subtlety is that you can have both unconditional and conditional heteroskedasticity. For instance, data from different regions might each have a different baseline variance (unconditional), but also that variance might fluctuate further in each region based on local conditions (conditional). Correctly distinguishing and modeling these behaviors is crucial for accurate forecasts and inference.

What is the effect of a very large sample size on heteroskedasticity detection?

As sample size grows, formal tests for heteroskedasticity gain statistical power. That means small deviations from constant variance may become statistically significant, even if those deviations are not practically relevant. In very large datasets, you might detect “heteroskedasticity” that is mild enough to have minimal impact on your conclusions.

This leads to a potential pitfall: focusing solely on p-values can cause you to overreact to trivial violations of homoskedasticity. The remedy is to complement your hypothesis test with an effect-size measure or to examine how your coefficient estimates and standard errors change when you switch to heteroskedasticity-robust methods. If robust inference yields nearly the same conclusions, the heteroskedasticity might be negligible in practical terms.

What domain-specific strategies exist for mitigating heteroskedasticity?

Depending on the domain, certain transformations or modeling choices can be more effective than generic approaches. In finance, log-returns are often used rather than raw prices, because price variance tends to grow with the price level. In medical cost data, you might log-transform the cost variable because high-cost patients have much larger variance than low-cost patients. In engineering stress tests, a square-root transformation might be suitable for data that scale in a certain geometric manner.

These domain-driven transformations often have theoretical justifications (like multiplicative errors becoming additive on a log scale). Another approach is to segment the dataset if you know certain subpopulations naturally differ in variance. For example, in insurance datasets, large commercial clients may have claims with far higher variance than small businesses. You might analyze them separately or include special variance terms or weighting for each subpopulation.

Each approach has edge cases, particularly if the transformation distorts interpretability. For instance, log-transforming the target can make the results harder to explain to stakeholders who expect predictions in the original scale. You must weigh the benefits of stabilizing variance against the cost of making the model less transparent or more complex to back-transform.