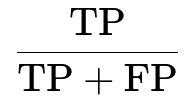ML Interview Q Series: How would you use a Confusion Matrix for determining a model performance?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

A Confusion Matrix is a tabular structure that summarizes the predictions of a classification model by comparing the predicted labels with the true labels. It is typically laid out in a 2 x 2 format for a binary classification task, capturing true positives, false positives, false negatives, and true negatives. These four quantities can be used to derive various performance metrics, including accuracy, precision, recall, and F1 score, among others.

It helps you see not only how many predictions are correct or incorrect, but also in what ways the model is making mistakes. For instance, you can determine whether your model is more prone to false positives or false negatives. This provides a clearer insight into the nature of your model’s performance than a single scalar metric like accuracy.

Key Metrics Derived from the Confusion Matrix

One major benefit of the Confusion Matrix is that it allows you to compute performance metrics in a direct and interpretable way. Some of the most commonly used metrics include:

Accuracy

TP stands for the number of true positives, TN for the number of true negatives, FP for the number of false positives, and FN for the number of false negatives. Accuracy indicates the proportion of correct predictions across all predictions. While it is simple and intuitive, it might be misleading in datasets with a large class imbalance.

Precision

Precision is the proportion of positive predictions that are truly positive. High precision suggests that when the model predicts positive, it is correct most of the time. This is crucial in situations where false positives are especially costly.

Recall

Recall measures the proportion of actual positives that the model correctly identifies. High recall implies that the model misses fewer positive instances. This is important in scenarios where false negatives are very costly (for example, in a disease screening context).

F1 Score

The F1 score is the harmonic mean of precision and recall and provides a single metric when you want a balance between the two. If precision and recall are both crucial for your task, the F1 score offers a good combined measure.

Practical Implementation

You can compute these metrics using many popular libraries such as scikit-learn in Python. Below is a simple code snippet that demonstrates how to calculate a confusion matrix and the associated performance metrics for a binary classification setting:

import numpy as np
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score

# Example true labels and predicted labels
y_true = np.array([0, 0, 1, 1, 1, 0, 1, 0])
y_pred = np.array([0, 1, 1, 1, 0, 0, 1, 0])

# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
print("Confusion Matrix:")
print(cm)

# Extracting TP, FP, FN, TN from the confusion matrix
# Assuming the convention [[TN, FP], [FN, TP]]
TN, FP, FN, TP = cm.ravel()

# Compute metrics
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)

print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

In the code above, the confusion_matrix function returns a 2 x 2 matrix. The first row corresponds to actual negatives, and the second row to actual positives. The columns correspond to predicted negatives and predicted positives respectively. By extracting these components, you can compute any custom metric desired. The scikit-learn library also provides built-in functions for calculating common metrics like accuracy, precision, recall, and F1.

How to Interpret and Act on Confusion Matrix Insights

The Confusion Matrix reveals where the model is making errors. A deeper look can tell you whether the model confuses one class with another. In practice:

If you care more about reducing false positives, you might try to increase precision or adjust the decision threshold to favor fewer positive predictions. If you care more about catching all positives, you focus on recall and can adjust the threshold in a way that yields fewer misses.

In cases with multiple classes, the confusion matrix generalizes to a larger square matrix where the diagonal entries represent correct classifications for each class, and off-diagonal entries represent misclassifications.

Follow-up Questions

Why might accuracy be misleading on imbalanced datasets?

Accuracy can be very high if you have a large majority class. For instance, if 95% of your dataset is labeled as negative, a model that always predicts negative for every instance would get 95% accuracy but fail to detect any positives. In such cases, metrics like precision, recall, F1 score, or other specialized metrics (such as the Matthews Correlation Coefficient or AUC) become more informative.

What is the benefit of looking at individual entries in the Confusion Matrix rather than focusing on a single metric?

A single metric such as accuracy or F1 might mask the nature of errors the model is making. By examining individual cells in the Confusion Matrix, you can determine if the model is disproportionately producing false positives or false negatives, or if there is confusion among specific classes. This level of granularity guides further model improvements, data collection strategies, or threshold adjustments.

When would you prefer precision over recall?

Precision is typically important when false positives are especially costly. In fraud detection, for instance, a false positive might inconvenience a legitimate user by blocking their transaction. In such scenarios, ensuring that positive predictions truly are positives is more critical than possibly missing some fraudulent cases. On the other hand, recall is vital when missing a positive instance is far more costly (for example, diagnosing a serious disease).

How do you handle multi-class classification with a Confusion Matrix?

For multi-class tasks, the Confusion Matrix grows to C x C dimensions, where C is the number of classes. Each cell (i, j) represents the frequency of instances from class i predicted as class j. To evaluate performance, you can compute overall metrics (macro-averaged, micro-averaged), or compute metrics per class and then average them. This helps identify which classes are most frequently misclassified and whether the model confuses particular classes.

Why might you use a threshold moving approach with the Confusion Matrix?

Many classifiers output probabilities or decision scores. A fixed threshold like 0.5 is not always optimal. You can adjust the threshold to achieve better recall or better precision, depending on the need. Plotting a Confusion Matrix as you vary thresholds lets you see how these changes affect the balance between false positives and false negatives.

Could a high precision and high recall model still be undesirable?

Sometimes a high precision and recall model might still fail in certain subgroups or under specific conditions not captured by the aggregate metrics. You might need to explore class-level breakdowns or look at segment-based performance. For example, if your data is skewed for different demographic groups or time periods, you might have good overall scores but poor performance on an underrepresented subset.

These considerations underline the importance of carefully interpreting the Confusion Matrix. It’s not only about getting high-level metrics but also about diagnosing error types, class imbalances, and threshold-related issues that might emerge in real-world use cases.

Below are additional follow-up questions

How can we extend the Confusion Matrix to handle multi-label classification tasks?

In multi-label problems, each sample can have multiple labels simultaneously. Instead of a single predicted label, the model outputs a set of labels (or probabilities for each possible label). A straightforward extension of the Confusion Matrix becomes less direct because you no longer have a strict one-to-one mapping between a predicted label and a true label.

One approach is to consider each label as a separate binary classification problem. For each label, you can compute a 2 x 2 matrix showing how often the model correctly predicts that label (true positive), incorrectly predicts it (false positive), misses it (false negative), or correctly omits it (true negative). This results in as many 2 x 2 confusion matrices as there are labels. You might then average the metrics (precision, recall, etc.) across all labels to get a global sense of performance.

A subtle issue arises if some labels have very few positive examples. In that scenario, average metrics might be skewed by labels with more examples. One must be careful with how metrics are aggregated across labels, because micro-averaging and macro-averaging can give different views of model behavior.

How does the Confusion Matrix help in a cost-sensitive classification context?

In many real-world scenarios, the cost of different types of misclassifications is not the same. For example, misclassifying a malignant tumor as benign (false negative) may be far more costly than misclassifying a benign tumor as malignant (false positive).

A Confusion Matrix helps in visualizing and quantifying these misclassifications. You could assign a cost to each cell (e.g., cost of false positives and cost of false negatives) and compute the total cost of your model’s predictions by summing over the Confusion Matrix cells weighted by their respective cost. This allows a more tailored metric that captures the real-world repercussions of each type of error. You might then tweak your model’s decision threshold or training procedure to minimize the total cost.

Pitfalls can occur if costs are estimated inaccurately. Overestimating one type of cost can bias the model to over-correct for that type of error. Also, real-world costs might be dynamic or context-dependent, so a single cost metric might not fully capture the changing environment.

Why might the Confusion Matrix look very different between the training set and the test set?

One of the main reasons is overfitting. On the training set, the model might learn patterns that do not generalize, resulting in an optimistic Confusion Matrix with a high number of true positives and true negatives. However, when evaluated on the test set, the model could show a higher number of false positives and/or false negatives due to less robust patterns or unobserved data distributions.

A shift in data distribution between training and testing (also known as dataset shift or distribution shift) can also cause discrepancies. If the test data differs in class balance, feature distributions, or underlying conditions, the Confusion Matrix might reflect errors that the model did not learn to handle during training.

Furthermore, label noise or poor data quality in either the training or the test set can yield mismatched Confusion Matrices. In practice, investigating such discrepancies involves checking for data leakage, verifying the sampling approach, and ensuring consistent data preprocessing.

What role does calibration play when interpreting a Confusion Matrix?

Many models produce a probability or confidence score for each prediction. However, the predicted probabilities might not be well-calibrated, meaning that a 70% confidence does not always translate to a 70% chance of being correct. Poor calibration can result in a confusion matrix that does not align with the raw probability outputs in an intuitive way.

Calibration curves or reliability diagrams can help assess whether the predicted probabilities match actual outcomes. If a model is poorly calibrated, adjusting the decision threshold or using techniques like Platt scaling or isotonic regression can bring the probabilities closer in line with reality. When the probabilities are well-calibrated, you can interpret them more directly, and the corresponding Confusion Matrix at any chosen threshold will reflect a more reliable trade-off between false positives and false negatives.

A common pitfall is to rely on uncalibrated probabilities to set thresholds for classification decisions in safety-critical applications. If the probabilities are overly confident or too conservative, you might see sudden spikes in certain Confusion Matrix cells that could have grave real-world consequences (e.g., missing many positive cases).

What happens if a class is never predicted? How do you interpret the Confusion Matrix in that scenario?

If your model never predicts a particular class (for instance, the positive class), then the confusion matrix row for that predicted class will be entirely zeros. This typically occurs if the model’s decision function or threshold is set such that it becomes overly conservative and avoids predicting that class. This often correlates with 0 precision for that class (since you predicted zero positive instances) and an undefined or zero recall for the class if there were actual positive instances you missed.

In practice, never predicting a class indicates a severe bias or threshold issue. For example, if the model learned that the positive class is extremely rare or costly to predict, it might default to predicting negative. Solutions include adjusting class weights, re-sampling the data (oversampling positives or undersampling negatives), or tuning the decision threshold so that it makes at least some positive predictions.

How should you handle a Confusion Matrix for ordinal classification tasks?

Ordinal classification tasks have classes that follow a natural order (e.g., ratings on a scale from 1 to 5). Standard confusion matrices do not capture the severity of misclassifications that are “close” versus “far” in the ordinal sense. For instance, predicting a 3 when the true label is 4 may be less egregious than predicting a 1.

Although you can still use a standard C x C matrix, it might mask the ordinal nature of the task. One solution is to attach penalties to misclassifications based on their distance in the ordinal scale, effectively creating a cost matrix. This modifies how you interpret the confusion matrix and might lead to different optimization strategies. For example, you could minimize the mean absolute error or mean squared error, each of which accounts for the magnitude of ordinal misclassification.

A subtle pitfall is forgetting that ordinal classes have a continuum nature, and using purely nominal metrics (like standard accuracy or F1) may not be the most appropriate way to measure performance.

How do time dependencies influence your interpretation of a Confusion Matrix?

In certain applications, especially time series classification or sequential decision-making, predictions happen repeatedly over time, and errors at one time step can propagate. A single confusion matrix on aggregated predictions may hide the temporal structure of these errors.

For example, if your model frequently predicts false negatives in a specific time window (say, early on in a process), you might need a time-segmented confusion matrix that reveals the pattern of misclassification over different intervals. Failure to see the temporal dimension could lead to misguided conclusions about the model’s stability or degrade real-time performance.

A related pitfall is retraining or updating a model over time without segmenting the data to see if earlier time frames have different confusion patterns compared to later time frames. Distribution shifts might occur gradually, causing the model’s errors to accumulate in specific ways that a single, aggregated confusion matrix will not reveal.

Why might you need separate confusion matrices for different subgroups of a population?

In many real-world scenarios, your data may contain distinct subgroups (e.g., different demographic groups, different product categories, or different geographic regions). The model might perform very differently on these subgroups, leading to equity or fairness concerns if one group experiences disproportionately higher false positive or false negative rates.

By computing separate confusion matrices for each subgroup, you can see if the model systematically makes more errors for certain categories. This might reveal the need for fairness-focused interventions or highlight how sampling imbalances are impacting model performance on a minority class. The pitfall here is ignoring these subgroup breakdowns, which might mask significant performance disparities behind aggregated results that look acceptable on the whole.