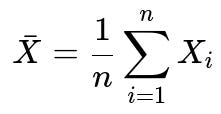ML Interview Q Series: When you sample, what potential Sampling Biases could you be inflicting?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Sampling bias arises whenever the process used to select data points or subjects for your sample misrepresents or systematically excludes key parts of the population. Such biases lead to samples that fail to capture the true variability and statistical characteristics of the full population of interest. This can be subtle or overt depending on how the data is collected, the sampling methodology, and the subject behavior during data gathering.

One of the simplest ways to illustrate the impact of sampling bias is by comparing the sample mean to the true population mean. When you draw a truly random, representative sample, the expected value of the sample mean is the actual population mean. Mathematically, for a random variable X with n observations X_1, X_2, ..., X_n, the sample mean (denoted X̄) is given by:

Here n is the sample size, and X_i is the i-th observation in the sample. If the sample is truly representative, the expected value of X̄ is the population mean. However, if we collect our samples in a biased manner (for instance, ignoring certain segments of the population), then the expected value of X̄ will deviate from the true population mean.

Below are common forms of sampling bias and why they occur in practice.

Coverage Bias

Coverage bias happens when the sampling frame fails to include certain segments of the population. If important subgroups are never considered in the sample selection procedure, the collected data no longer represents everyone but only those within the frame. For example, surveying opinions via a web-based form can exclude people without stable internet access, automatically creating a coverage bias.

Selection Bias

Selection bias arises when individuals or observations are chosen in a way that is not random, thereby systematically favoring certain outcomes or types of data points. In real-world scenarios, selection bias often sneaks in if participants have to opt into a study or if data is gathered from a non-random set of sources (e.g., only sampling from certain neighborhoods, certain age groups, or certain times of day).

Non-Response Bias

Non-response bias occurs when a significant number of selected subjects fail to respond or drop out, and their absence is not random. For instance, if a survey is about sensitive topics (like personal finances or health conditions), and those who feel uncomfortable with the topic systematically refuse to participate, the survey results will be skewed.

Self-Selection (Voluntary Response) Bias

Self-selection bias is common in situations where individuals voluntarily choose to be part of the sample. People with strong opinions (positive or negative) are more likely to respond compared to those who are indifferent. This phenomenon is frequently seen in online polls or feedback forms, where you usually get responses from those who feel motivated to share their opinions, not a balanced slice of the entire user base.

Survivorship Bias

Survivorship bias occurs when only “survivors” or successful observations remain in the sample, leading you to draw conclusions without considering entities that did not “survive.” In a business context, for instance, analyzing only companies that exist today and ignoring those that went bankrupt or closed will produce misleading views on strategies or success rates.

Healthy User Bias

In medical or health-related studies, healthier or more proactive individuals are more likely to participate in certain programs. If researchers only look at participants in the health program and do not account for the fact that they may differ systematically from the broader population, the results will be skewed.

Recall Bias

This occurs when participants in surveys or interviews are asked to recall past behaviors or events, but some groups recall information more (or less) accurately. This discrepancy in the ability to remember events can introduce systematic error that distorts results.

Potential Real-World Impact of Sampling Bias

Biased samples can lead to misinformed decisions and inaccurate models. In machine learning projects, data that is not representative can cause your models to perform poorly on real-world data. For instance, a face recognition system trained mostly on images from a single demographic group will underperform (often dramatically) on other demographic groups. Similarly, a fraud detection system that only learns from a skewed set of transaction data might fail to generalize once deployed.

Practical Strategies to Minimize Sampling Bias

Ensuring that the sampling frame represents the full population is often the first major step. When possible, random sampling procedures (e.g., simple random sampling, stratified sampling) help achieve more representative samples. Stratified sampling, for instance, intentionally divides a population into subgroups (strata) and samples proportionally from each stratum to maintain balanced representation. Consistently checking for significant differences in collected samples versus known population statistics is also a key part of any good data collection pipeline.

How to Detect and Diagnose Sampling Bias

One way to diagnose sampling bias is to compare your sample distribution to any available demographic or distributional data of the broader population. If these distributions differ significantly (for example, in age, income, race, region, or any relevant factor), it is a sign of sampling bias. Another approach is to run sensitivity analyses by excluding or focusing on specific subgroups within your sample to see if results change drastically. Unusually large changes can be a symptom of underlying bias.

Follow-up Questions

Can you give an example of how you would correct for sampling bias once your data has already been collected?

In some cases, you can use weighting or post-stratification. If you have external information about the population distribution (e.g., you know that 30% of the population should come from a certain demographic group, but in your sample, that group is only 10%), you can assign weights to each data point to reflect the overall distribution. However, such a correction can be limited by what external data you have and how accurately you know the true population proportions. You must also be careful: weighting can improve representativeness on known demographic features but might not fix unknown biases. Another approach is to collect additional data from underrepresented groups to rebalance the sample if it is feasible.

How can sampling biases affect model performance in machine learning?

Models trained on biased samples will often generalize poorly. They might achieve high accuracy on the biased dataset but fail in the real world. For example, if your training data underrepresents certain classes, the model might struggle when encountering those classes in production. This leads to higher error rates and can manifest as fairness issues (e.g., systematically discriminating against certain groups). Ultimately, sampling biases can undermine trust in the model and result in costly decisions, especially if you deploy the model at scale.

What techniques can help ensure that data pipelines remain unbiased over time?

Monitoring and drift detection are crucial. Even if your initial dataset was representative, real-world data distributions can shift over time (called concept drift). Maintaining a pipeline that periodically checks whether input data distributions match past distributions helps detect biases that might be creeping in. In addition, implementing a continuous feedback loop where you periodically retrain your model with fresh data can help the model adapt to changing patterns. If there are subpopulations of critical concern, you may incorporate bias detection tools that look specifically at model performance and data distributions for these subgroups.

How might biased sampling appear in an online A/B testing scenario?

In A/B testing, if only certain types of users are funneled into the experiment or if the experiment is run at times that exclude certain time zones, biases can emerge. For example, if you run an A/B test in a region where users have certain browsing habits or demographics that don’t match your overall user base, the result might not reflect broader user preferences. Another issue is self-selection bias when users opt into the test (or into certain features) instead of being randomly assigned. These biases may lead you to adopt a feature that only a subset of users like, and later it fails to perform well with the entire user base.

How do you address non-response bias in practical data-collection scenarios?

One approach is to follow up with non-respondents or incentivize them to participate. Incentives can be monetary or in the form of services or additional benefits. Another approach is to compare early respondents to late respondents. If late respondents more closely resemble non-respondents, you can try to understand the differences in responses, which may help you adjust or weight your data accordingly. In some settings, you might do an auxiliary survey with a small fraction of non-respondents to estimate how their responses differ from those who responded.

In what ways can domain knowledge mitigate sampling bias?

Domain knowledge is essential in identifying subgroups or factors that might be systematically excluded from your sample. An expert understanding of how data is generated, how participants are recruited, or how events occur in the real world can help you spot biases that might not be obvious from a purely statistical perspective. For instance, a domain expert in healthcare may know that certain symptoms or conditions go underreported in specific communities, so they can guide efforts to oversample or specifically include those groups.

By carefully accounting for these various forms of sampling bias, data scientists and machine learning engineers can build models and draw conclusions that are far more robust, trustworthy, and fair in real-world applications.

Below are additional follow-up questions

How can we quantitatively measure and diagnose sampling bias in a dataset?

A thorough approach to measuring sampling bias often involves comparing the distribution of the sample against known or assumed characteristics of the overall population. In practice, you can use statistical tests—like a chi-square test—to compare categorical distributions (for example, comparing the proportion of different demographic groups in your sample to census data) or a Kolmogorov–Smirnov test for continuous distributions. If there is a statistically significant difference, it might indicate that certain subpopulations are over- or under-represented.

A subtle pitfall here is lacking a clear idea of the true population distribution, which can happen if you do not have reliable external data. In such cases, domain expertise is critical to make an educated guess about who or what might be missing. Another issue arises if there is a temporal aspect to your data—maybe your population changes drastically over time, so current external data is not a perfect reference for historical samples. Careful validation with multiple data sources or time-sliced analyses can help mitigate such challenges.

Could data augmentation help with sampling bias, and what are the challenges?

Data augmentation typically refers to synthetically enlarging a dataset (e.g., rotating or flipping images in computer vision tasks) or creating small perturbations to textual data for NLP tasks. While this can help bolster representation of rare classes or scenarios, it does not necessarily fix a fundamental sampling bias if entire subpopulations or behaviors were never captured. Augmentation can sometimes introduce artificial artifacts if it goes beyond small realistic transformations.

A subtle pitfall is generating augmented samples that do not match real-world conditions. For instance, if you artificially increase minority-class examples through heavy transformations, your model might learn features that do not generalize well to genuine data. Hence, while augmentation can partially address class imbalance (related to sampling bias in classification tasks), it is not a silver bullet for broader sampling biases where entire distributions of behavior or demographic groups are missing.

How might sampling bias manifest itself when there is a mismatch between training and test data distributions?

If your training data is collected from one source (say, users from a specific geographic region or a particular time period), but your test data (or future production data) comes from a broader population, you risk encountering significant errors in production. Your model might appear to perform well on the training set but fail when faced with new types of examples not represented in training.

A key pitfall is failing to notice that performance metrics (like accuracy or F1 score) will look healthy on a biased validation set but plummet when encountering new subpopulations. Another issue is the mismatch may be subtle—for instance, user behaviors that shift seasonally or across different cultural contexts. Periodic re-checks of performance across multiple segments (geo, time, device type) are critical to detect and handle such mismatches.

How do you handle sampling bias when there is no way to collect additional data?

In scenarios where data collection is no longer possible—perhaps due to cost constraints, privacy considerations, or time limitations—various post-hoc adjustments become the fallback strategy. One approach is weighting samples if you have some prior knowledge of true population proportions. Another approach might involve model-based correction methods where you explicitly include variables correlated with underrepresented groups. You might, for instance, create features that indicate which subset of data each sample belongs to, so the model can learn to correct or adapt for known biases.

The major pitfall is that these fixes rely on assumptions that might not be completely correct, especially if you do not have good reference data about the population. Weighting can inadvertently amplify noise in the underrepresented samples. Additionally, if key subgroups are entirely absent, there is no direct way to remedy that. In such cases, the best strategy is to acknowledge the limitation and be transparent about which segments the model may not handle reliably.

Is an extreme class imbalance in classification tasks always due to sampling bias, and how might you address it?

Class imbalance can stem from both natural phenomena (e.g., fraud being inherently rarer than legitimate transactions) and sampling design (failing to capture enough minority-class instances). Not all class imbalance is a direct result of sampling bias; sometimes it genuinely reflects real-world event frequencies. If the imbalance arises from your sampling procedure, the best fix is to improve how you sample. If it is a genuine property of the domain, you can adopt techniques such as cost-sensitive learning, oversampling minority classes, undersampling majority classes, or using appropriate performance metrics (e.g., precision-recall over accuracy).

A subtle pitfall is conflating a natural imbalance with a sampling problem and attempting to “fix” it by artificially balancing classes in ways that no longer reflect real-world frequencies. This can degrade real-world performance because the model sees an unrealistic proportion of minority-class examples. Balancing classes must be coupled with clear metrics that reflect costs and benefits of different error types.

What is the difference between sampling bias and data drift, and how do they interact?

Sampling bias is a systematic error in how data is selected or collected, whereas data drift refers to the phenomenon where the statistical properties of the target variable or feature space change over time. If you have sampling bias at the outset, your model might be built on non-representative data. Then, as the real-world distribution shifts (data drift), your model may perform even worse because it never captured the original distribution accurately, and now that distribution is changing further.

A key pitfall is attributing deteriorating performance solely to data drift, when in fact the original dataset was also biased. Monitoring for drift (like checking feature distributions over time) is essential, but you also need to make sure the baseline distribution you are comparing against is representative in the first place. If your baseline is flawed by sampling bias, the diagnosis of drift might be misleading or incomplete.

Can sampling bias still occur in unsupervised learning, and how do you detect it?

Even without labels, if you collect data from skewed sources, the resulting clusters or dimensionality-reduced embeddings can be unrepresentative of the true population. For instance, if you are using clickstream data but only record interactions from a subset of devices, you might cluster user behaviors that reflect only those device-holding users. Detecting bias in unsupervised settings often involves comparing cluster characteristics or distributions to external knowledge. If clusters systematically exclude known segments of the population, it is a red flag.

A pitfall arises if you rely purely on internal metrics (such as silhouette score) without examining how the data aligns with what you know about the broader domain. Another subtlety is that some biases may hide within high-dimensional data in ways that do not appear in the reduced dimensionality or cluster results. Continual domain awareness and partial label or demographic data can be crucial for uncovering and mitigating such biases.

How can you systematically diagnose sampling bias in a multi-source data pipeline?

Many real-world systems pull data from multiple channels—logs, surveys, transactions, third-party APIs. Each source can have its own biases. A systematic diagnosis starts by mapping out each data source and identifying how data flows into the pipeline. Then, for each source, you check whether certain subpopulations or event types are systematically excluded. You might compare the distribution of each source to a reference population or to each other.

One subtle pitfall is assuming that merging multiple biased sources fixes the problem, but in practice, biases can compound. For example, you might have a user base from Source A that skews toward a certain demographic and a user base from Source B that skews another way, leading to complex combined distortions. Another challenge arises in weighting each source if you are attempting to build a unified dataset. If you do not weigh them carefully, you might still be amplifying one bias more than others. A thorough approach involves exploring cross-tabulations of key attributes (region, device type, user segments) across all sources and validating them against domain-specific expectations.